课堂速递
【Date:2022.05.20】
网课不停歇,居家也要学好数学。我们数学组的老师们为了给每位光华学子们在网课期间学好数学,“数位板”“几何画板”“电容笔”“真人小视频”为了拉近和学生们的距离,呈现原汁原味的实景教学,可谓无所不用其极。两个月网课下来,“鼠标大王”绝对名副其实。
万人期待的3月14日的“数理派 实力派”节活动由于疫情影响,被突然搁置,那些同学们的”名画”也只能被“雪藏”,那些激动人心的游戏项目也需等待再次相逢才能开启。现在为了弥补数理派节活动的遗憾,于是隆重推出光华中学“数学故事会”,跟着我们的老师同学一起涨知识。
“他年届40岁才偶然见到几何。在一位绅士的图书馆里,桌上有一本打开的欧几里得的《几何原本》,正翻着卷I的命题47处。他读完这条命题,便提高了嗓门—他时常会以这种方式强调他在赌咒发誓—说道:这是不可能的!于是,他读了该命题的证明,可这又引导他去求助于前一条命题;他读前一条命题的结果是他还得再往前求助于另一条命题……,最后他彻底相信了那条真理,这一经历使他喜欢上了几何。”
——引自奥布里《小传集》
前文中的主人公是哲学家托马斯.霍布斯。感兴趣的同学们你可以猜猜他读的是哪条定理?

你猜对了吗?就是毕达哥拉斯定理,而这段故事则展现了希腊数学奉献给数学中一种最重要的力量“演绎方法”,因为强大的因果关系,就可以让推理无懈可击,更可以让你摸清事物的真相。为了让各位同学们明白这种几何中蕴含的奥秘,喜欢上那种抽丝剥茧,顺藤摸瓜般找到真相的感觉,老师才“百般折磨”让七年级写证明题加上理由(定理),这样到了八年级证明题才能把因果关系梳理正确,而后九年级证明题过程就可以达到严谨二字了。(找到这段话中的几层因果关系了吗?)
打开了脑洞,就跟随小编进入这一期的“数学故事会”。
1
故事一:勾股定理
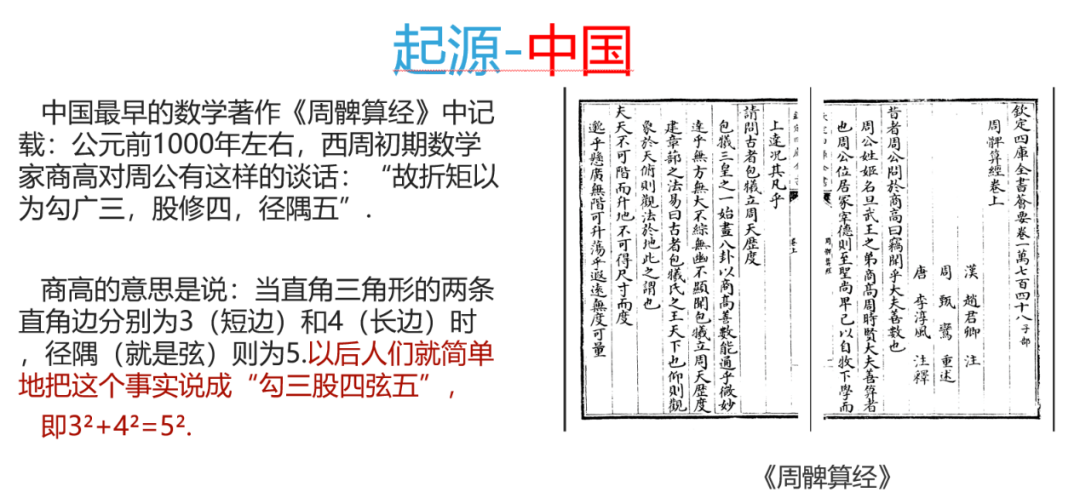
上文中的毕达哥拉斯定理又被称之为勾股定理,那么勾股二字何义?首先,我们就跟随七(2)班李韧康同学来到三大文明古国中国,古埃及,古巴比伦,由他来为我们揭开《勾股定理》的神秘面纱。
2
故事二:祖冲之与割圆术
如果说勾股定理(毕达哥拉斯定理)展现出了演绎证明的完美,那么无限和无穷的概念绝对在希腊数学中如同“禁忌”般的存在。在西方对于“无限和无穷”望而止步之时,我们东方一颗冉冉的巨星正在升起,那就是祖冲之与他的“割圆术”,割圆术的出现以及穷竭法的诞生则让人明白了对于无限和无穷探索的意义,让更多数学家为之痴迷。下面就由6(3)班叶雅绮带来的《祖冲之与割圆术》。

3
故事三:爱在坐标系
如果说毕达哥拉斯定理第一次暗示了在算术和几何之间隐藏很深的联系,那么接下来那位著名矿泉水广告人物笛卡尔将把算术和几何用解析几何这一独特的方式完全联系在一起。让我们一起来跟着七年级李潇贝、张倩菲两位同学的步伐走进笛卡尔那种“我思故我在”的神奇意境:

七(1)班李潇贝、张倩菲两位同学为同学们讲“爱在坐标系”的故事
小编补充:
笛卡尔对才智方面的对手没有雅量,即他对当时科学巨人伽利略,费马和帕斯卡等怀有敌意,而非常鼓励年轻人不断发挥自己的数学才能,喜欢和能够理解自己思想的人沟通交流,所以这才有去瑞典当女皇的私人教师的故事。所以不要盲目崇拜科学巨人,他们也是普通人。
4
故事四:欧拉与他的小故事
历史上有一位数学家,可以不用眼睛做数学题,出版的《代数》一书现在也是数学教科书之一,他就是欧拉,又一位数学界的大神。作为本期数学故事会的最后演讲成员,他们是来自六年级的黄一鸣,梁琳轩和董雅玉,一起来看看他们是如何精彩演绎欧拉著名的《七桥问题》:

本期数学故事会就到这里了,从毕达哥拉斯定理到割圆术的出现,从笛卡尔到欧拉,你涨了多少知识呢? 如果看到这里,那么你一定涨了很多知识,那就请把这份知识收藏(下方有个方块),收藏了那么好的东西是不是应该分享呢?既然分享了是不是就该点赞了(大拇指需要你)呢?点赞了的你一定会期待下一次由光华中学八九年级的学长们带来数学故事会了。
最后,想想多久没有和你的小伙伴讨论“压轴题”争执“ABCD”了,多久没和你的老师近距离“过招pk”了?让我们一起再次祈祷疫情早日过去,相会光华。