最近同学们在积极准备期末考试,之前在高强度微积分计算中信手拈来的一个自然底数e,反而在同学们高频复习对数和指数运算部分时常常被这个小“e”使了绊子,似乎计算的基本法则也还算清楚,但是一顿计算操作下来打心底还是想单纯的问一句无关智商的话:老师,e到底是啥,e到底是怎么来的?
对于感觉似乎越学越糊涂的你但凡能问出这句话,高低我得夸你两句。

毕竟,你会掠过现象看本质遵从第一性原理从源头开始思考了。
常数e的出现是我们高中学习生涯中掌握的为数不多的特殊常数,并且亲切的称之为自然常数。
准确的说常数e是从指数函数的章节引入学习的,但是在课本中的出现似乎是那么的突然那么的淡然以至于才有了同学们的不知其所以然。

俗话说:一个神秘的符号按照剧情发展必定有它背后的一段神秘故事;
俗话又说:一个神秘故事必定成就了一个C位男主角。

那么,剧情渲染到这今天故事的男主角的剧照高低要给大家剧透一下了。

(转自百度)

(转自百度)
伯努利一身功与名,今天且看如何鼓捣常数e....
伯努利是个数学家,没事就在家鼓捣数学问题,有天他研究到复利问题(compound interest),通俗点来说通过银行的利率怎么捣鼓“一本万利”的事情。

好家伙,这数学家就是高智商,净琢磨人在家中坐,钱到头上来哈!
捞银行油水如下:

常规油水:第一年本金存储为a元,银行支付年利率100%,则年底获取本金综合为2a
非常规油水:如果我们调整100%利率的发放次数,按照每年两次每次50%来发放,我们看年底收益:a(1+50%)(1+50%)=2.25a
如果我们调整100%利率的发放次数,按照每年四次每次22.5%来发放,我们看年底收益:a(1+22.5%)(1+22.5%)(1+22.5%)(1+22.5%)=a(1+22.5%)4≈2.44a
如果我们调整100%利率的发放次数,按照每个月复利一次,那么到年底将发放a(1+1/12)12≈2.61a
伯努利发现有搞头,俗话说“人有多大胆,地有多大产”,这次来个狠的直接一步到位:如果把这个计息次数无限细分下去,那么最后年底不就会得到无穷多的钱,这不就是妥妥的真真的闷声发大财,想想心里心里偷着乐!
伯努利大概快乐了3s,想着想着毕竟是个数学家,还是要对结果严谨负责的,于是在纸上写出了下面的极限表达式
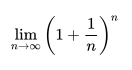
现在同学们定睛一看,这个让人产生一夜暴富幻想的式子学过微积分的同学并肯定不陌生了,这个不就是我们讲过的特殊极限么,他的极限将会最终收敛于一个无限不循环小数,即我们后来定义这个数为常数e
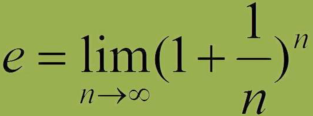
至此,常数e的出身终于清白了,原来常数e表示的是某种复利增长模型的极限。
故事虽小,也算闻道,
愿你保持学习的兴趣
用思考探索更多未知!

END