
本学期,数学组和艺术组合作开展了一次与非具象艺术相结合的上海星河湾双语学校G1G5G7数学活动。在活动中,同学们感受到了来自几何与艺术相结合的美。
在G1和G5的日常教学中,同学们学习了各类几何图形,例如点、线、三角形、四边形和圆。G7学习了包含平面和曲面的立体图形,及其展开图和表面积、体积的相关计算。在艺术课堂中,同学们接触了荷兰画家蒙德里安的非具象绘画。若是将两者结合,同学们会迸发怎样的奇思妙想呢?
在G1数学活动中,我们从学生的成果作品中看到了具体到抽象(将现实中具体的事物抽象出其本质特征并用数学语言表现)、从整体到分块的结构(将现实中的整体分解成由各种元素所构成的部分),这些既是数学思想体现也是艺术的表达形式。

G5的数学活动还结合了多项主题进行展开,如细胞、司南、树木等,分别对应了科学、中国传统文化和现实世界,同学们在活动中打开了更多想象的空间。
G7的数学活动巧妙渗透了二维及三维图形的联系和变化。首先,学生通过二维的展开图、三视图,和表面积计算,学会表示立体图形的不同方法;其次,学生可以探索多面体的面、边和顶点之间的联系;最后,学生创造性地设计组合立体图形模型,以此来表现具体和抽象的联系和变化,更加深入地体会了几何世界的魅力。
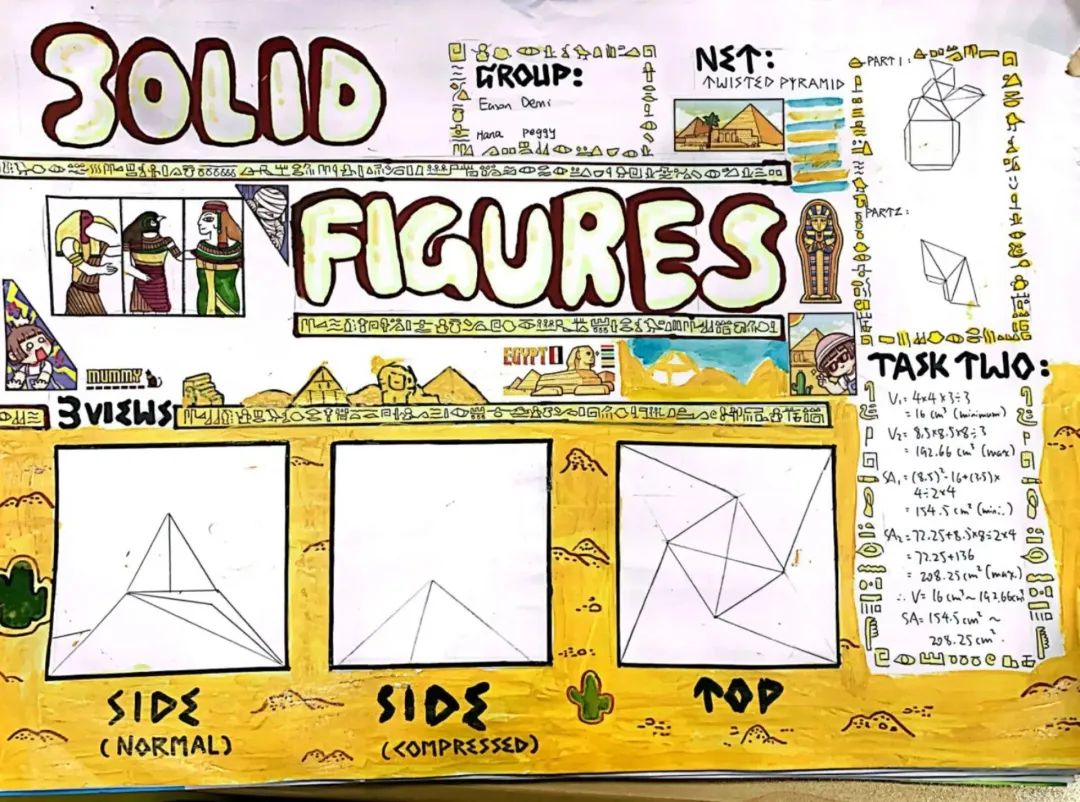
在本次数学活动中,G7的同学们不仅深切感受到了立体几何之美,也锻炼了观察、计算和作图能力。每个小组的作品都让老师们惊喜不已,他们不仅分享了设计思路,而且充分展现了空间想象力和独特的创造力。
本学期数学教研组精心设计的学科活动受到了广泛欢迎,不仅让学生能把所学的知识应用于生活,运用多种方式感知、应用数学知识,体验创造的乐趣,而且也培养了他们的动手操作能力,独立思考、团队合作、创新设计能力,激发了学生对数学学习的浓厚兴趣。
In this semester, the math group carried out a mathematical activity combined with art. In the activity, the students felt the aesthetics from the combination of geometric art and mathematics.
In our daily teaching, G1 and G5 learn all kinds of geometric figures and concepts, such as points, lines, triangles, quadrilateral shapes, circles, and so on. G7 learned the solid figures, including flat and curved surfaces, nets and the related calculation of surface area and volume in the mathematics class. In the art class, the students were exposed to non-figurative paintings by the Dutch painter Mondrian. If you combine the two, what kind of wonderful ideas will you have?
From the G1 and G5 students' paintings, we can see the concrete to the abstract (abstracting the concrete things in reality from their essential characteristics and expressing them in mathematical language). From the whole to the block structure (dividing the whole in reality into parts composed of various elements), which are the embodiment of mathematical ideas. In addition, this activity combines a number of themes: cells, compass, trees. It corresponds to science, Chinese traditional culture and the real world respectively. Students in the activity, have more imagination and play of the space.
This G7 project skillfully integrated important mathematical thoughts such as modeling, relationship and representation. First of all, students used nets with dimensions, three views, and surface area calculations to represent the mathematical information about the models from different perspectives. Secondly, they explored the connection between faces, edges and vertices of a polyhedron. Finally, they creatively designed compound models to represent a concrete object or an abstract intention, and further understood that mathematics is the way to represent the real world.
During the activity, the students not only deeply felt the beauty of solid geometry, but also exercised their ability to observe, calculate and practice. In the end, the teachers were surprised by the works presented by each group, and they also expressed and shared their design ideas. Each group representative fully demonstrated their spatial imagination and creativity through clear and complete expression.
In a word, this subject activity carefully designed by the mathematics teaching and research group is very popular with students. It not only enables students to apply the knowledge they have learned to life, perceive and apply mathematics knowledge in various ways, and experience the fun of creation, but also cultivates their hands-on ability, independent thinking, teamwork, innovative design ability, and arouses their strong interest in mathematics learning.