模联社 - 强大社员，强大社团 MUN: Strong members make a strong club

上海宏润博源学校模拟联合国队 (SHBS MUN Team) 是一个由学生自主创办的学术竞赛队伍，汇集了来自全校各个年级的优秀学生。模拟联合国队伍成员包括6名各个年级前3，6名全A生，正在迈向一个追求完美，追求精英的学生组织。模拟联合国队旨在“为未来外交官提供展示平台”，秉承“为天地立心，为生民立命”，并不断地自我更新，创造奇迹。

由于模拟联合国活动的特殊性，大部分的训练内容很难在线上展开，创始人蔡晗啸同学和社员们把目光放在了基础知识的学习上。线上学习的2个多月来，他们系统性地学习了“形式逻辑”，有效地提高了各自的批判性思维能力。平时的学习内容由蔡晗啸创作并讲述，梁雨凡、吴文昊两位社团书记进行记录并整理。他们说：“我们整理的形式逻辑讲义尽管不能做到完全系统、专业，但也与此同时可以以通俗的方式让基础薄弱的同学快速入门形式逻辑。在此分享于学校公众号，欢迎对模拟联合国项目有兴趣的同学研读，也借此以飨读者。”

 

1)      Father of formal logic: Aristotle

2)      Case: William: Sam, who are you talking with?

 Sam: I’m talking with nobody

 William: Who’s “nobody”?

Analyzation: Here, William played a linguistic game on “names” vs. “quantifiers”

3)      Names ≠ quantifiers

4)      Some examples for quantifiers: nobody[0人], somebody[若干人], everybody[群体中的一个人]

5)      In language, none is none. 在语言中，没有就是没有

 

I. Names vs. Quantifiers

              A. “Nobody” is a quantifier that represents the state of non-existence.

              B. “Existence” and “non-existence” exist.

              C. Q: Is nothing something?

Both nothing and something are quantifiers. However, nothing represents the state of non-existence while something represents the state of existence.

              D. Postulate[公理；假设，假定]

                Postulates are non-provable beliefs.

                     Eg1. Postulate: A line is straight.

                     Eg2. Segment Addition Postulate.

       II. Basis of logic

A.    Truth value/ validity[有效性]（中性词）{negative=invalid; positive= valid}

a.       Proposition[命题]

Positive = √

Negative= ×

                           

B.     Conditionals & their validity

Conditionals(条件句): If…then…

a.       The assumption before “then” is a premise[前提条件].

b.      The conclusion after “then” is a  conclusion.

e.g.: Conditional         a. If Leo joins MUN, then, he’ll get smarter.

-validity: negative. Since smart= IQ and IQ of a person cannot be changed.

→ If Leo joins MUN, then, he’ll get more rational.

-validity: positive

 

b. If Charlotte practices calligraphy every day, then, she’ll improve her skill.

                              -validity: positive.

                     Conditional: If…then…

c.       4 types of validity for conditional

   i.              Positive

  ii.              Negative

  iii.              Deductive[推论有效性]

  iv.              Inductive [归论有效性]

III. Family of conditional

                            条件句

                                     If… then…

1.      Converse: A. If a, then b. / B. If b, then a   逆命题

2.      Inverse: if a, then b. / If not a, then not b. not: a negation否命题

3.      Contrapositive: If a, then b. / If not b, then not a.  逆否命题

 IV. “Or” & “And”

p∩q => p and q  “∩”and

p∪q => p or q       “∪”or

 

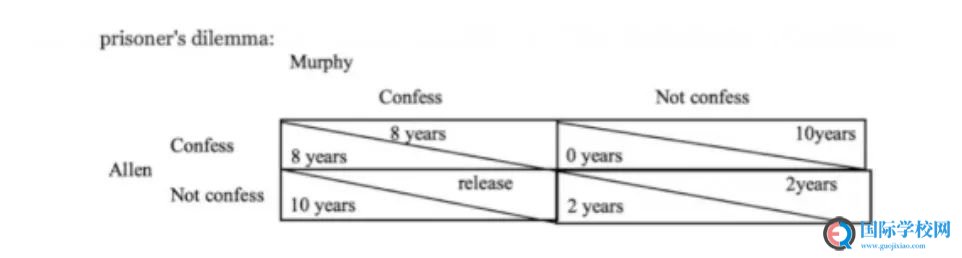
If Murphy has chosen to:        Confess             Not confess

Then Allen’s best choice:        Confess                Confess

 

If Allen has chosen to:            Confess            Not Confess

Then Murphy’s best choice:    Confess                Confess

 

Truth table 真值表

Truth table: to represent all the kinds of relationships between two objects.

 

1

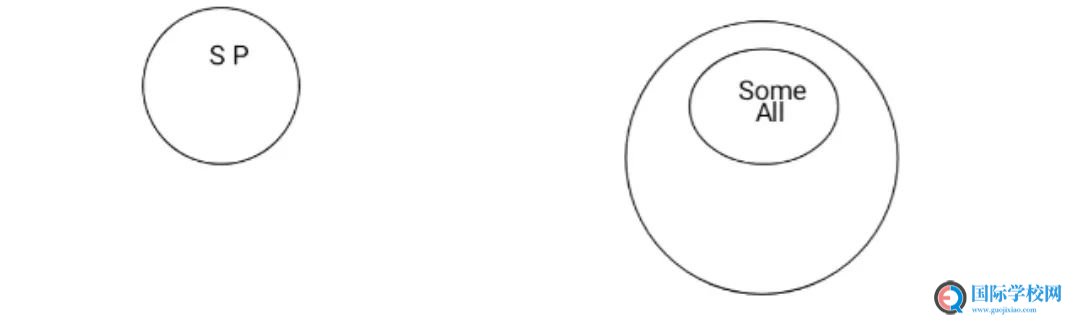
In this picture, s, p have a non-contiguous relation (不接壤关系)

It means whatever s or p is, they have no relationship.

2

In this picture, s, p has a sharing part

 It means some part in s and p is same

3

In this picture, s is bigger than p and p is included in s

It means all p is in s but there is still other part in s

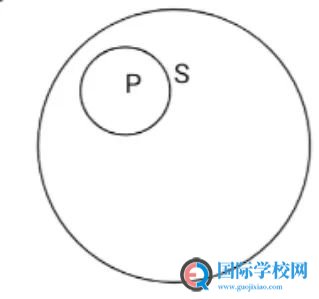
4

In this picture, s is p

It means the description of s is the description of p

Here is the problem which we met in the class

Does “some” equals to “all”?

The answer is yes because “some” is belonged in “all”

 

 

Name                   Meaning             Notation         Example

Negation(负命题)          No(并非；不)           ¬              ¬P

Conjunction(联言)         And(并且；和)        ^               p ^ q

Disjunction(选言)          Or(或者；要么)  ∨          p∨q

Conditional(假言命题)     If…then (如果…那么) →         p → q

 

Understand the meaning of every notation and know how to use it